Catalog of No Three Deductions: A Setter's Perspective

Contents

• Background
• Connectivity
  • Connectivity at the Corner
  • Connectivity at the Edge
  • Connectivity Elsewhere
  • Grounding
  • Miscellaneous
• One-Line Deductions
  • NT1: Four Basic Forms
  • NT2: Invisible 1 in 1x2
  • NT2 + Connectivity
  • NT3 + Grounding
  • NT4: Natural Occurrence
  • Miscellaneous
• Two-Line Deductions
  • N in 2xN
  • NT1/1, 2/2: Mirroring
  • NT1/2, 2/3: Anti-Mirroring
  • Three Violation Forms
  • Miscellaneous
• Three-Line Deductions and Above?
  • Penalty Theory
• Double Coverage
• Band Theory
• Summary

Background

This is a non-comprehensive catalog of deductions in No Three, the Nikoli pencil puzzle with the quirk of prohibiting three evenly spaced shaded cells in a row (or column). I will assume that you're already familiar with the rules of the genre; if not, Puzzle Square JP has the rules and as well as a number of puzzles to get you started. What this catalog focuses on is to (re-)introduce many of the deductions already discovered in No Three, as of January 2024, from the perspective of a setter. If you're only interested in solving, you may not find this article highly informative, though I still hope to present the genre as reasonable -- as one that relies on delectable logical reasoning as opposed to dry scanning, the way most people initially feel. But if you care enough to consider setting your own No Three puzzle one day, I want to give you the most holistic view possible of the genre so far, including which deductions have proven useful in constructing, and which deductions have not been explored enough where new variations may be found.

Like any interesting pencil puzzle, No Three is host to a wide variety of deductions, ranging from trivially easy to considerably difficult. It would be a waste of time trying to catalog them all. We need some sort of criteria for deciding which deductions are deserving of our attention. We intuitively feel that some deductions are "better" than others, but how do we know, for sure?

Of course, the answer ultimately boils down to aesthetics, since puzzling is, after all, an aesthetic pursuit. On the other side of the same coin, however, some deductions are strongly favored by almost all setters, and come up over and over again in actual puzzles. There seem to be some measure of the "merit" of a deduction itself.

To make this idea more concrete, I propose the concept of cost. It's not a scalar quantity; just a way to measure the relative ease of implementing one deduction over another. For instance, I will use words like expensive or costly to indicate that a deduction is, in general, difficult to implement in real puzzles; while a cheap deduction is one that is versatile and reusable across many different situations. The estimation of cost is partly based on attributes I will introduce shortly, and partly based on empiricism, which is anything but exact. As a result, I will refrain from abusing this term, and employ it only when it serves to illustrate a point.

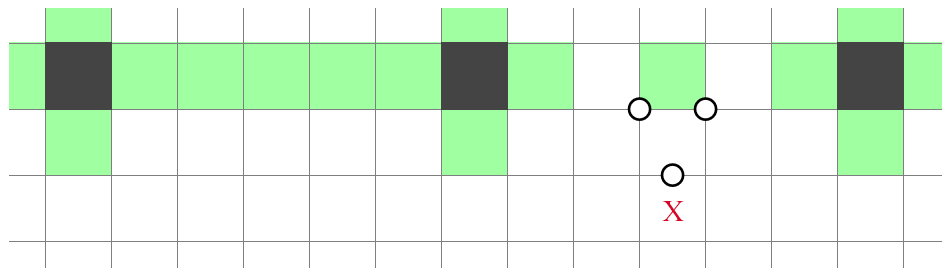
Time to get puzzling. The following figure exemplifies of an expensive deduction in No Three:

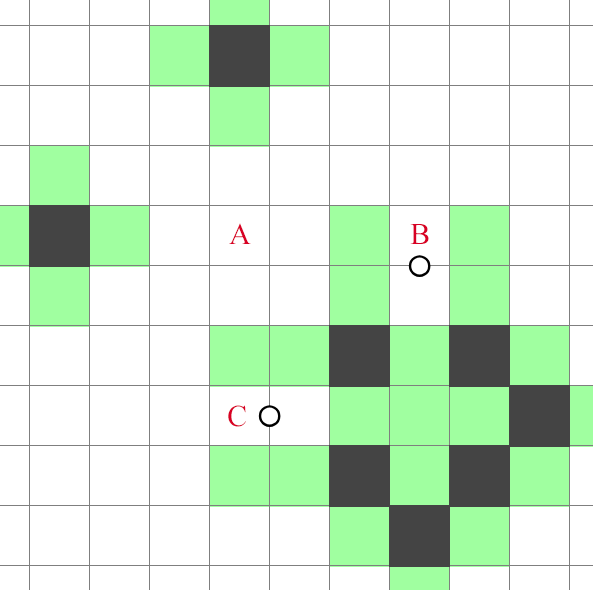
To begin with, let's examine how this deduction works through lookahead -- the most fundamental and generic approach in all of logic puzzle reasoning. All deductions can be considered glorified lookaheads; however, it is a task more suited for computers, not the human brain. We don't like to solve puzzles by doing a multi-layer exhaustive search. We like to solve puzzles by extracting clean patterns and understanding them at a high level, which is why we have "deductions" in the first place. Nevertheless, we will often need to use lookahead, because deductions are far from sufficient to cover all situations.

If we shade the cell marked with $A$, then by the no-three-in-a-row rule (which I will abbreviate as the NT rule henceforth), we must not shade the cells marked with $B$ and $C$. As a result, the unshaded area at the bottom right will be completely surrounded by shaded cells, which is a violation of the connectivity rule. We thus conclude that cell $A$ must be unshaded.

However, if we attempt to implement this deduction in an actual puzzle, some problems would immediately arise:

• This deduction takes up a lot of space. We have to allocate a an entire 9x9 square for this deduction, which limits the number of other deductions we can include and restricts the layout of the whole puzzle.

• This deduction has an irregular shape. Regular shapes such as a rectangle allow a deduction to fit neatly between other deductions, and allow for chaining (more on this in later sections). An irregular-looking deduction requires that you plan for it at the very beginning of the construction, not later.

• This deduction gives us little information. We only learn, through this deduction, the status (shadedness or unshadedness) of a single cell, which means that as a setter, we must insert additional clues into the gaps to fully resolve the rest of the 9x9. This process is highly error-prone, especially to bypassing -- that is, after introducing new clues, the solver may be able to determine the status of other cells first, and then come back to unshade $A$, completely negating (or bypassing) the entire deduction. The following figure shows an example of how it might go:

  

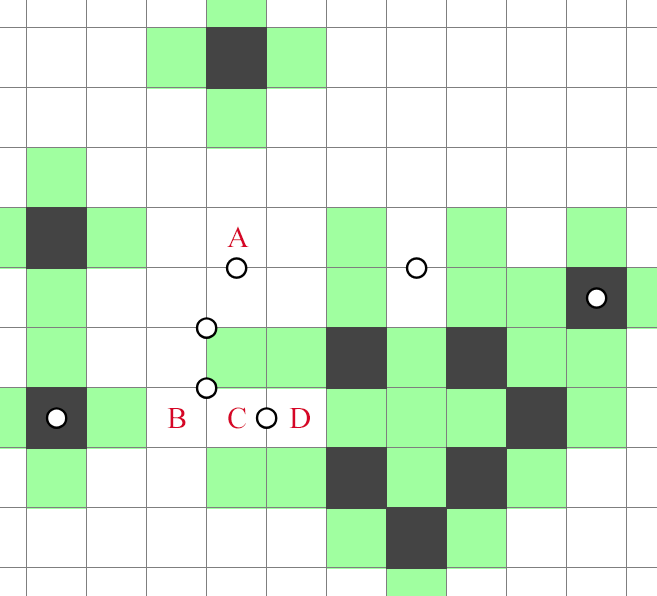
  In order to resolve the undecided cells, I hastily added some clues to the area, with the intention that after you unshade $A$, you will have a dichotomy between shading either just $C$, or both $B$ and $D$. The latter case is a contradiction due to the shaded cell on the left, which means $C$ must be shaded. But wait! It turns out that I accidentally forced $D$ to be unshaded independent of the other cells, which then gives you the status of $C$, and lastly $A$ -- my intended deduction is totally bypassed!

  This is the sort of situation you will often come across as a setter, doubly so if you're implementing an expensive deduction. Great attention to detail and a lot of backtracking are necessary to ensure that no solver can bypass your deductions.

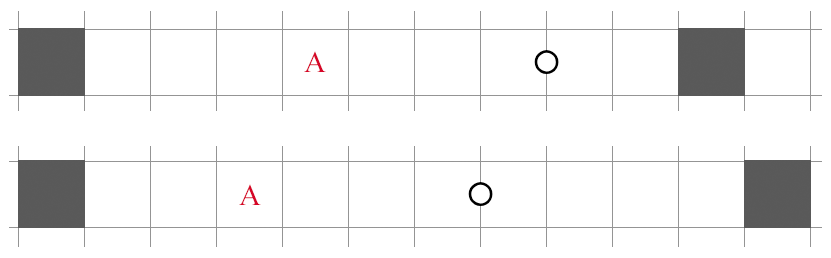
By contrast, let me now demonstrate a cheap deduction:

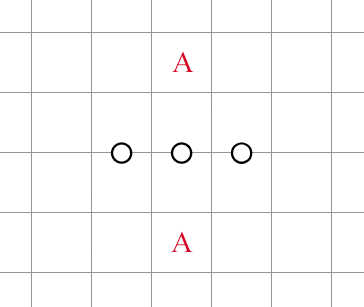
In this case, both cells marked with $A$ must be unshaded (which, again, can be concluded after a lookahead on either $A$). But you will probably immediately recognize that this is an instance of the iconic "N in 2xN" room in Heyawake. This deduction is quite popular in both genres because:

• It is compact. It occupies a tiny rectangular 2x3 area, which enables it to fit into all sorts of tight spaces, as well as chaining with other deductions.

• It is informative. Allowing us to unshade two cells may not seem like much information, but note that there are only two ways to shade the entire 3 in 2x3:

  

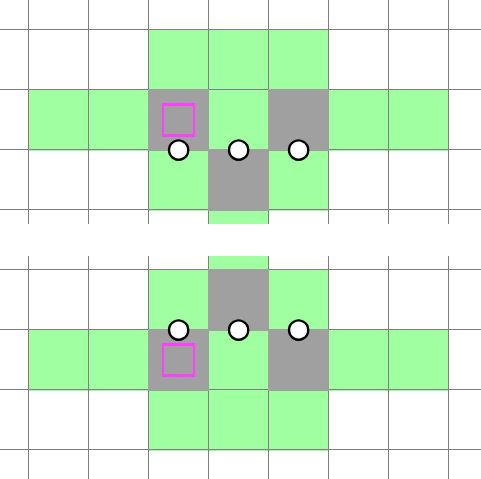
  When a structure can only be shaded in two ways, I call it binary. Binary structures can be easily decided by external influences and are very handy for constructing lookahead deductions. More on this later.

It should be clear that we care more about low-cost deductions than high-cost ones. Yet is the former kind inherently better than the latter kind? Not really. Apart from the fact that cost is not absolute, it only implies that expensive deductions take more time and effort to implement, not that they are impossible. And from the solvers' point of view, expensive deductions can be just as interesting and delightful to solve as cheap ones, not to mention that they will grow bored if all puzzles contain the same set of deductions.

Then what's the point of discussing cost at all? In my opinion, the abstract concept of cost can provide an important point of reference for designing what the solve path will look like. Hence, in this catalog, I will cover mostly cheap deductions, as well as a number of expensive ones, but I will make sure to mention their cost when necessary.

Connectivity

The reason I put connectivity in the first section is that there's not a great deal to say about it in isolation. As a common feature of Dynasty genres (an informal name for the class of shading puzzles that have "no adjacent shaded cells" and "unshaded cells connected" as rules), connectivity has myriad applications depending on specific circumstances, and it really shines when used in conjunction with other deductions. Therefore, I will defer some noteworthy connectivity reasoning to later sections where other deductions are discussed. However, I will list some basic "raw" connectivity applications here:

Connectivity at the Corner

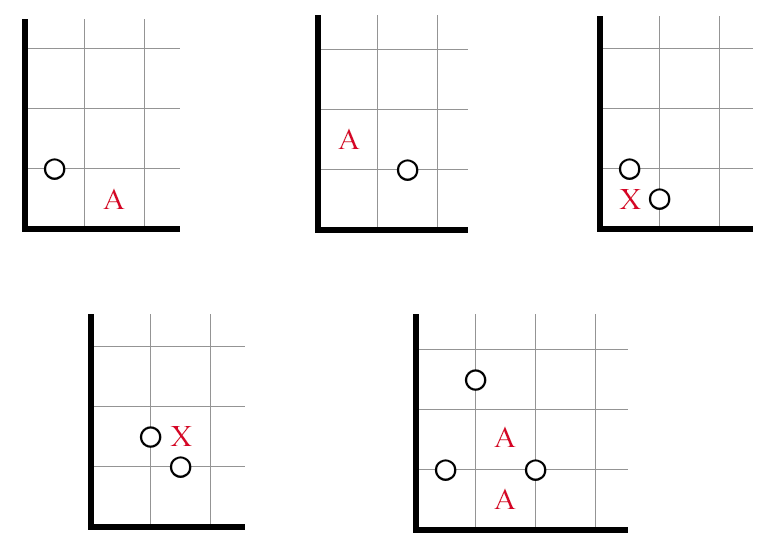
As a shorthand and convention, I will use the letter $A$ to mean that the cell must not be shaded and the letter $X$ to mean that the cell must be shaded, in each of the given scenarios. (I was going to use $O$ for unshaded, but that looked too much like the clue circle.)

Connectivity at the Edge

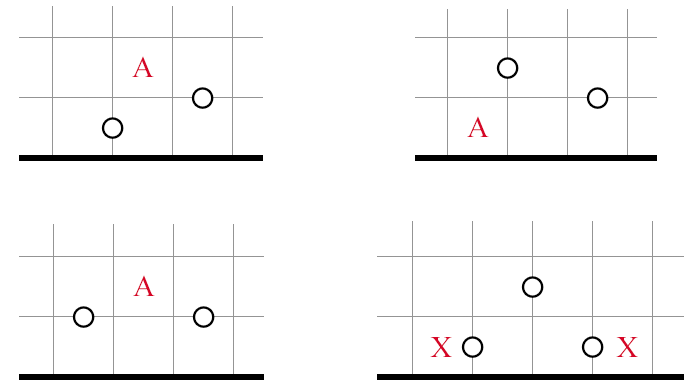
Connectivity Elsewhere

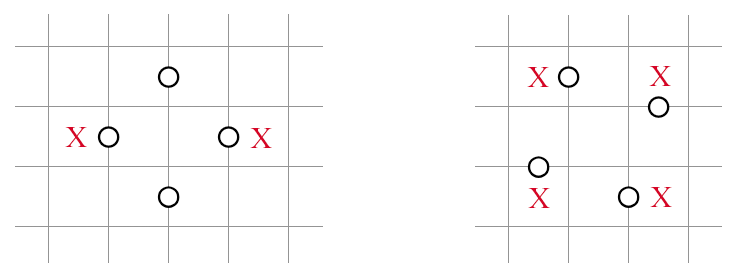
The last structure is sometimes referred to by Japanese puzzlers as the "windmill."

Grounding

The idea of grounding originates from Heyawake. A shaded cell is grounded if there exists a path of diagonally connected shaded cells from the cell to any edge of the board. The key is that you don't need to know which path brings the cell to the edge: you just need to know that there is one. And if there is one, there can't be another, because that would split the unshaded cells on the board in two. In the following figure, the shaded cell on the 1 clue is grounded at the bottom; if $A$ were shaded, it would be grounded again at the left. So $A$ must not be shaded.

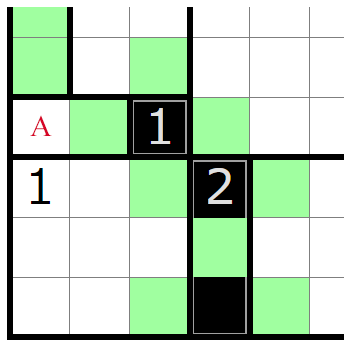
Can grounding extend to No Three? Unfortunately, not very readily. Grounding owes much of its success in Heyawake to the border rule that prevents a line of unshaded cells from crossing 2 region boundaries; there is no direct equivalent in No Three. In general, it's possible to implement grounding deductions in No Three, but it tends to be expensive, especially if you want the chain to be long. The following is a minimal grounding example:

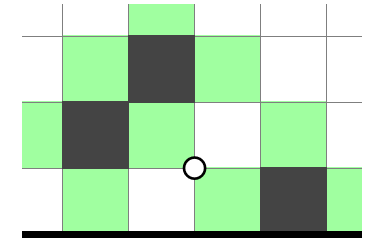
The concept of grounding will be revisited in later sections.

Miscellaneous

Here is a structure that is somewhat uncommon:

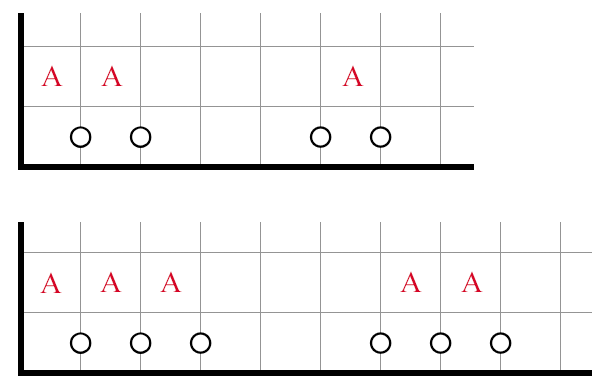
One-Line Deductions

The deductions in this section all concern the NT rule, particularly within a single row or column.

NT1: Four Basic Forms

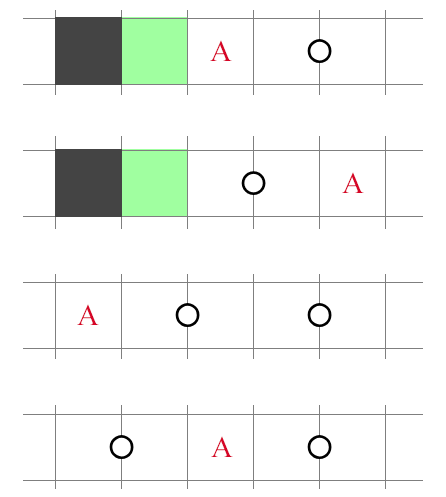
If there is such a thing as a "canonical" form in No Three, it has to be these four. They are the simplest and cheapest deductions beyond direct rule application, exploiting the smallest possible NT violation -- where three consecutive shaded cells are spaced out by a single cell. I will call this violation NT1 for short. By extension, there are also NT2 violations, NT3 violations, and so on. These four constructions fit just about anywhere and are a staple of the genre.

NT1 Extensions

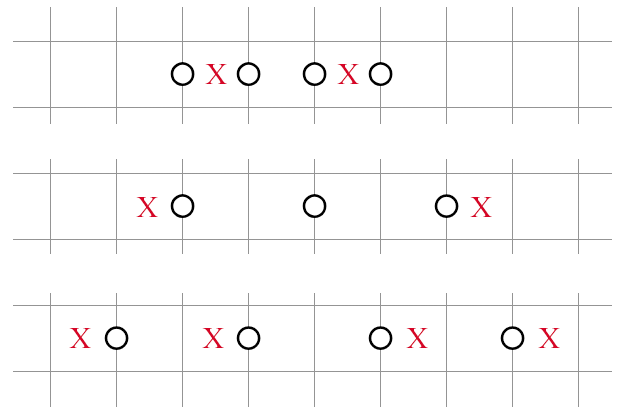
NT1: Diagonal Variant

This is a modification of the canonical NT1. Since all unshaded cells in the figure must be pre-determined externally, it's significantly more expensive to implement.

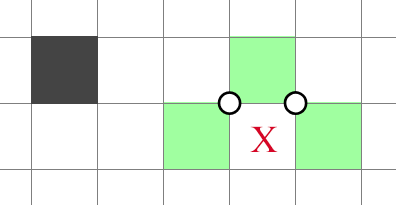
NT2: Invisible 1 in 1x2

In this construction, the cells marked with $B$ cannot both be shaded, or it would be an NT2 violation. So one of the cells marked with $C$ must be shaded, effectively creating an invisible clue in the middle. As a setter, you can use the invisible clue wherever you would use a normal clue.

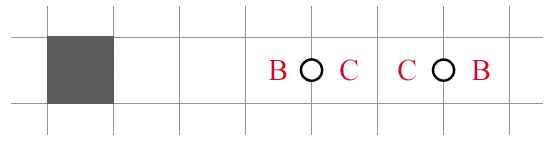
NT2 + Connectivity

This is an example of connectivity in conjunction with NT2. If $A$ were shaded, then $B$ would be too, which is a violation. This deduction is slightly expensive, as $A$ being unshaded is not much information.

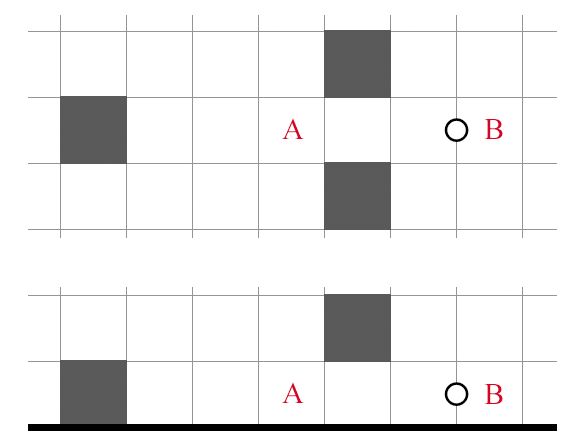
NT3 + Grounding

Here is another example of grounding. Cells marked with $B$ can't both be shaded, so cell $C$ is grounded. This deduction is fairly expensive: you cannot arbitrarily extend it upwards like you could in Heyawake. It would be a challenge to use it more than a handful of times in the same puzzle.

NT4: Natural Occurrence

Up to NT3, whenever you have two out of three consecutive shaded cells in the same line, you can immediately unshade the other cell that would cause a violation if shaded. However, it is perfectly valid to have three shaded cells in a row spaced out by 4 cells, provided that you shade at least one other cell among them.

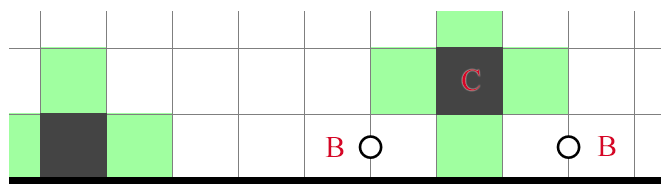
In the Japanese puzzle community, this is sometimes called "natural occurrence," referring to the phenomenon that the solver often doesn't notice until an NT4 has "naturally" occurred, at which point the solver has to "break" it in the middle. The most common application is as follows:

One of the cells marked with $B$ must be shaded, which in essence creates another invisible clue. Again, this 1 in 1x2 can be combined with anything else for a composite deduction.

A few remarks. First of all, NT4 requires the board to be at least 11 cells long in either dimension -- width or height. If the board is 10x10, as it is by default on puzz.link, NT4 cannot be implemented.

Secondly, NT4 (and above) is the only rule in No Three whereby a cell not touched by a clue can provide information. Barring NT4, there would be no rule dictating that you shade an untouched cell; and because of uniqueness, every untouched cell would have to be unshaded. NT4 gives the solver a reason why they would ever want to look at an untouched cell.

What about NT5 or higher?

They are expensive. NT5, for instance, demands at least 13 cells in one dimension of the board (which tends to make the puzzle cumbersome), and the pattern is peculiar. NT5 or higher are rarely seen in real puzzles.

Miscellaneous

Here are a few uncommon deductions in one row.

NT2+3

Deductions involving NT2 and NT3 in sequence. Unshading $A$ does not offer valuable information, so they are costly.

NT1+4

An even rarer deduction. If you look into two (or even more!) NT violations in a row, there are more possibilities, but they are usually prohibitively long.

Two-Line Deductions

N in 2xN

There are three different clues in No Three: the cell clue (1 in 1x1), the edge clue (1 in 2x1), and the intersection clue (1 in 2x2). By lining up N copies of the edge clue, we get a binary N in 2xN room.

3 in 2x3

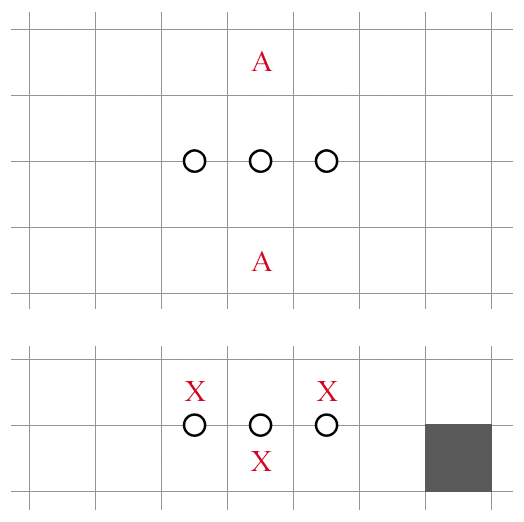
For $N \geq 3$, the middle cells in the row immediately above and below the room must be unshaded, which amounts to $N-2$ unshaded cells on each side (a deduction directly inherited from Heyawake).

However, what No Three distinctively possesses is the ability to determine 3 in 2x3 by a shaded cell to the left or right of the room. In the figure above, one way of shading the room would lead to an NT1 violation. When solving No Three puzzles, it's a good idea to keep an eye on the cells off to the side, in case a shaded cell pops up.

4 in 2x4

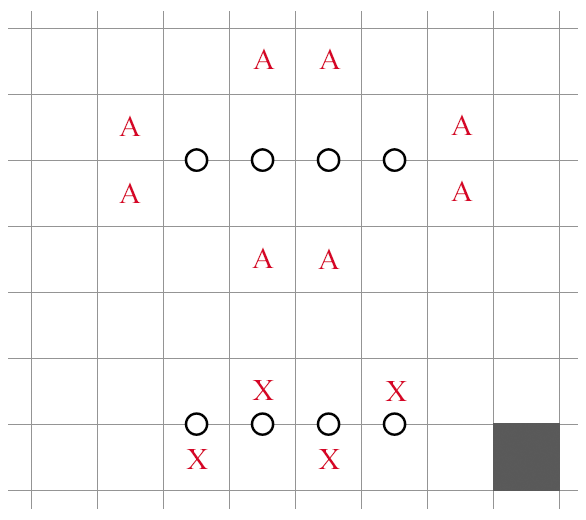
The same reasoning applies to 4 in 2x4 as well. In addition, all four cells on the left and right sides of the room must be unshaded due to NT1. An implication of this is that, unlike in Heyawake, there cannot be 5 in 2x5 or larger rooms in No Three. The obvious extension:

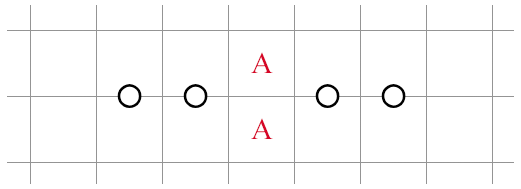
More on 3 in 2x3

3 in 2x3 is special in that it can be combined with a variety of other binary structures to form larger constructions. For example, the following figure shows a "3-1" binary structure that is decidable by a shaded cell two cells to the right through an NT2 violation:

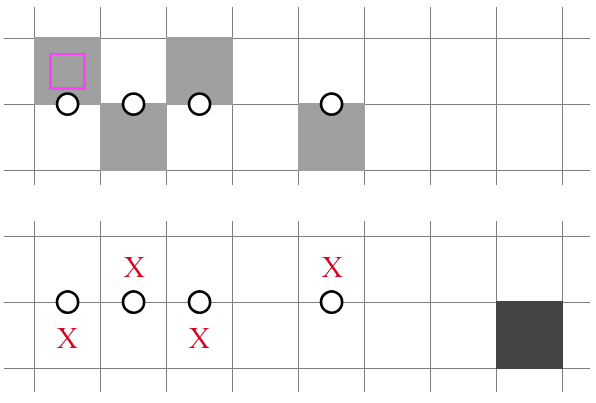
The deduction may not be easy to memorize as a solver, but if you can quickly identify a structure as binary, a lookahead could promptly yield progress. This is why binary structures are desirable in setting.

In a similar fashion, the following binary "3-2" structure is also decidable by an outside shaded cell through NT2:

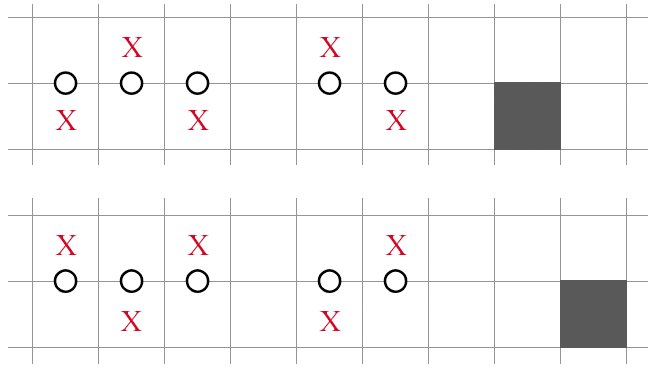
Moreover, here is another rare variation:

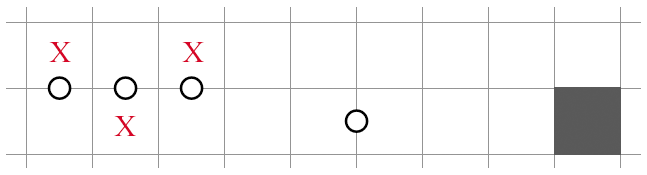
N in 2xN + Connectivity

These are all classic deductions inherited from Heyawake, derivable via lookahead. Especially the last one -- massive connectivity across whole boards is favored by many.

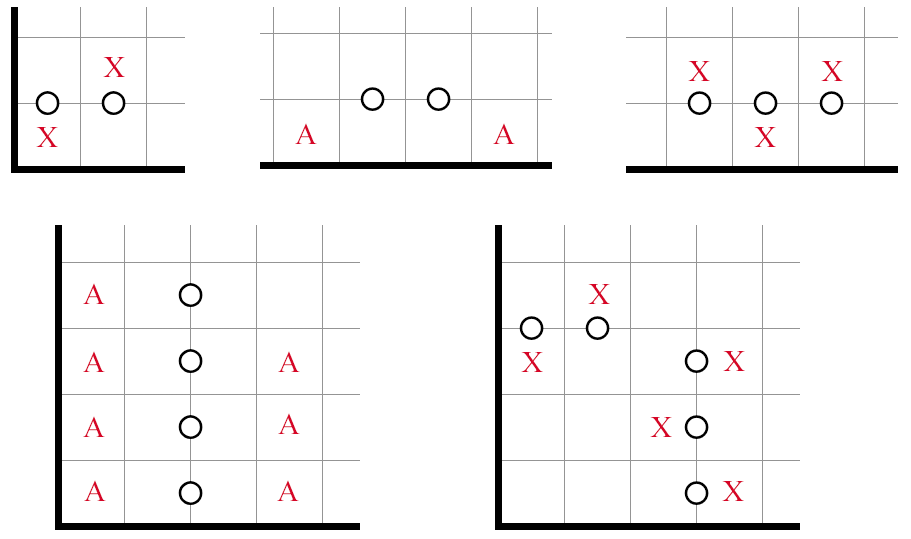
NT1/1, 2/2: Mirroring

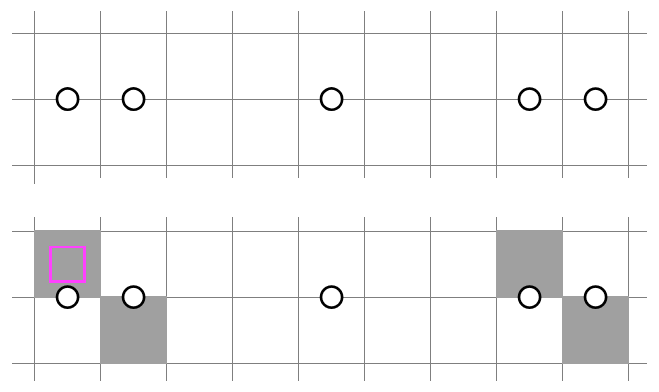
This is an interesting binary structure. If you tentatively shade the 2 in 2x2 on either side, you will find that the other one must be shaded in the opposite manner -- otherwise, after applying NT1 to both rows, the middle area would be fully unshaded. Consequently, the two 2 in 2x2's can be thought of as "mirror images" of each other, with the middle clue being the "mirror," hence the name "mirroring." The other part of this section's title, NT1/1, refers to NT1 being applied to two consecutive rows, with the slash representing the row separator.

Mirroring is extendable to both sides being 3 in 2x3, where it relies on NT2 twice (so I call it NT2/2):

There are two approaches to implementing mirroring in real puzzles. The usual way is to decide one side through external influences, and then use mirroring to decide the other side. However, you can also exploit the structure's binary nature and devise a lookahead. The following is an instance of mirroring (NT1/1) coupled with connectivity:

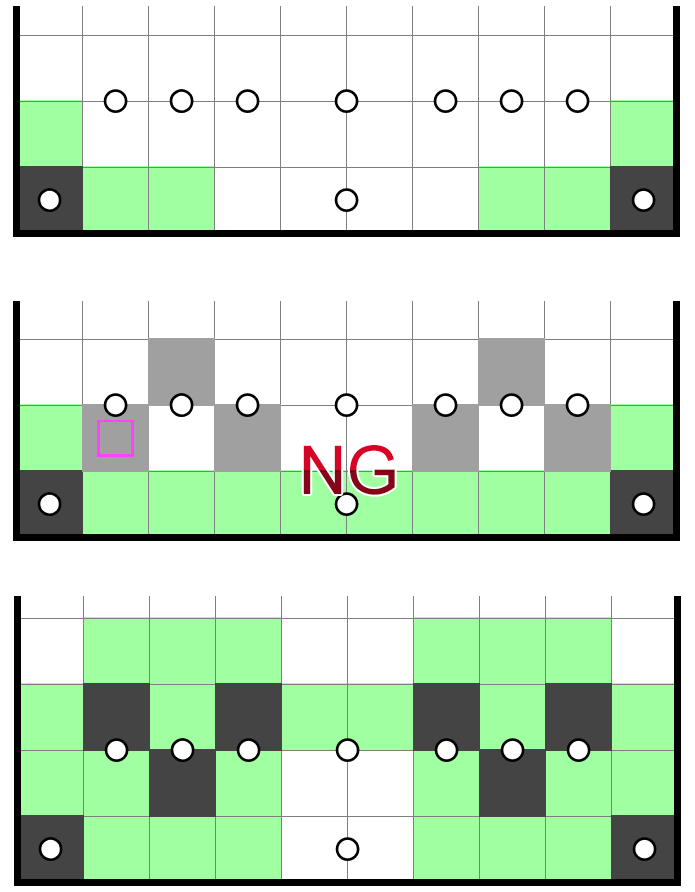
Mirroring can also be chained. As I mentioned earlier, cheap deductions that occupy a regular chunk of space have the nice property of being able to fit elegantly into other deductions, allowing for long lookaheads. The following incomplete example demonstrates a binary structure comprising four 2 in 2x2's:

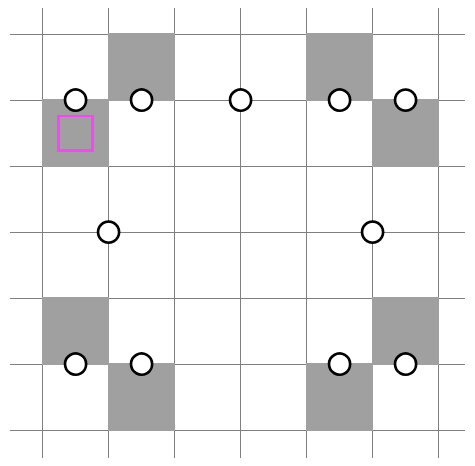
To resolve this structure, simply add clues so that one of the two possibilities leads to a contradiction.

NT1/2, 2/3: Anti-Mirroring

Amusingly, this binary structure is pretty much the opposite of the previous one. The central clue ensures that the pair of 2 in 2x2's must not be mirror images of each other -- otherwise, after applying NT1 and NT2 to the rows respectively, the middle would be wholly unshaded. I like to think of the central clue as the "anti-mirror," or you can think of the two sides as "clones" of each other.

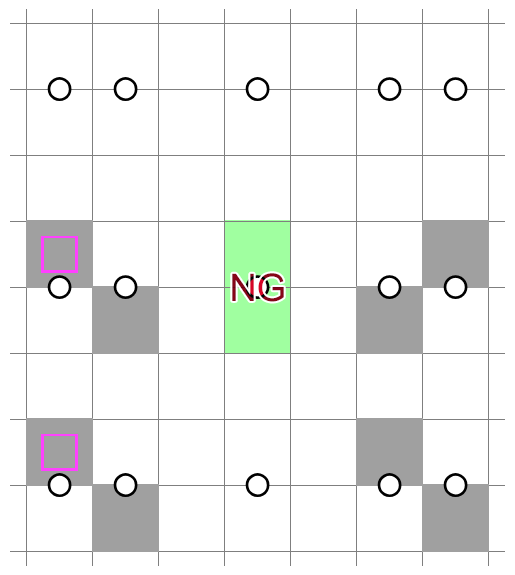
The gaps between the two areas can be widened, resulting in anti-mirroring (NT2/3):

Note, however, that it cannot be automatically extended to NT3/4, as NT4 alone is not a violation.

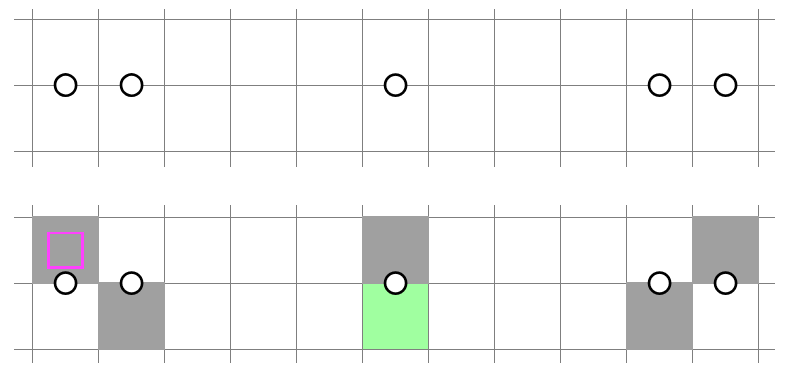
It is nevertheless possible to implement NT3/4 given that all the cells in between are unshaded through external influences. It is also possible to implement NT1/4 and NT2/4, albeit at great expense, as shown below:

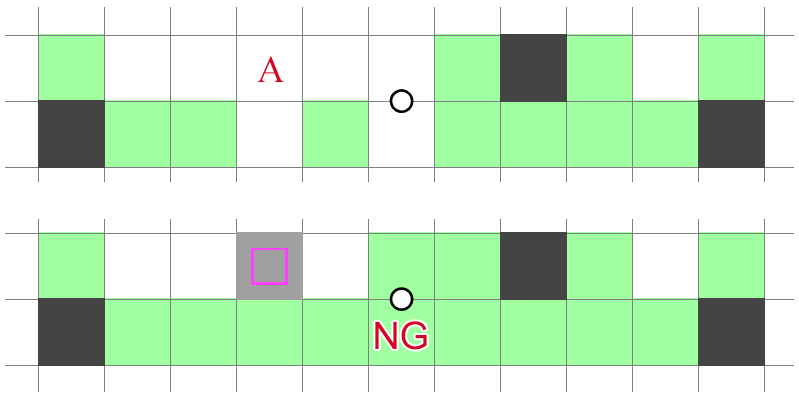
Anti-mirroring can also be implemented as a binary lookahead, and it is chainable, though perhaps not as elegantly. The following figure presents an implementation that combines anti-mirroring with grounding (where cell $B$ is grounded):

Footnote: The earliest known use of anti-mirroring on Puzzle Square JP was by ぴくちゃ, who called this deduction (in Japanese) Picture's Special.

Three Violation Forms

This is a curious class of structures that defy all attempts to shade them.

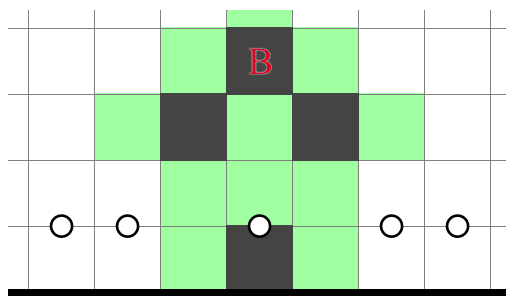
1-3-1

There appear to be two ways to shade the middle 3 in 2x3, but either way it would result in an NT2 violation. The structure is thus invalid.

To implement 1-3-1 in an actual puzzle, all you have to do is remove any one of the offending clues, and the corresponding 2x1 region must be unshaded:

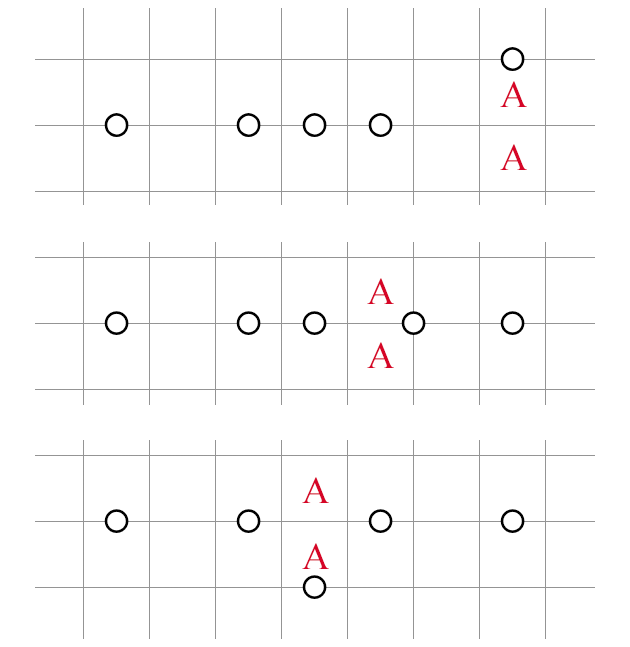
3-1-3, 3-2-3

The other two violation forms are 3-1-3:

And 3-2-3:

They can be implemented in the same fashion.

What is it that makes these constructions invalid, really? You may notice that both 1-3-1 and 3-1-3 include the 3-1 binary structure, whereas 3-2-3 includes 3-2, and I think this is one way to explain it. Binary structures are strict -- so strict that if the constraints are just a teeny bit too tight, they would fail to produce any solutions at all. Meanwhile, 4 in 2x4 doesn't show up in violation forms because it practically "cuts off" the two sides from each other, preventing long NT violations from occurring.

Violation forms can be implemented as lookaheads.

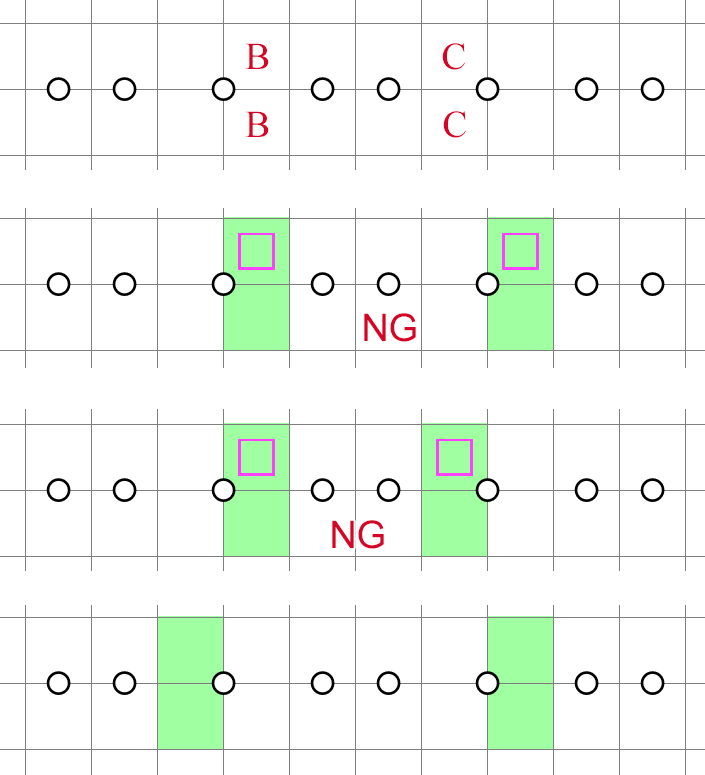
In this instance, consider how the $B$ cells might be shaded. If they're both unshaded, we can perform another lookahead on the $C$ cells to discover that they cannot be shaded -- or it would cause a 1-3-1 violation. Yet the $C$ cells also cannot be unshaded -- or it would cause a 3-2-3 violation. This contradicts our premise, and we can conclude that the $B$ cells must be shaded. The same argument can be applied symmetrically to the $C$ cells, and we see that they are shaded as well.

Alternatively, since this structure is also a chained mirror (NT1/1), we can obtain the same information by looking ahead twice on the 2 in 2x2's. What's more, we can just use an ordinary lookahead on any of the four unshaded cells and apply symmetrical reasoning both horizontally and vertically to arrive at the same place. Nevertheless, the point of having violation forms is to reduce the workload, as it would other be difficult to decide which cells to look ahead on.

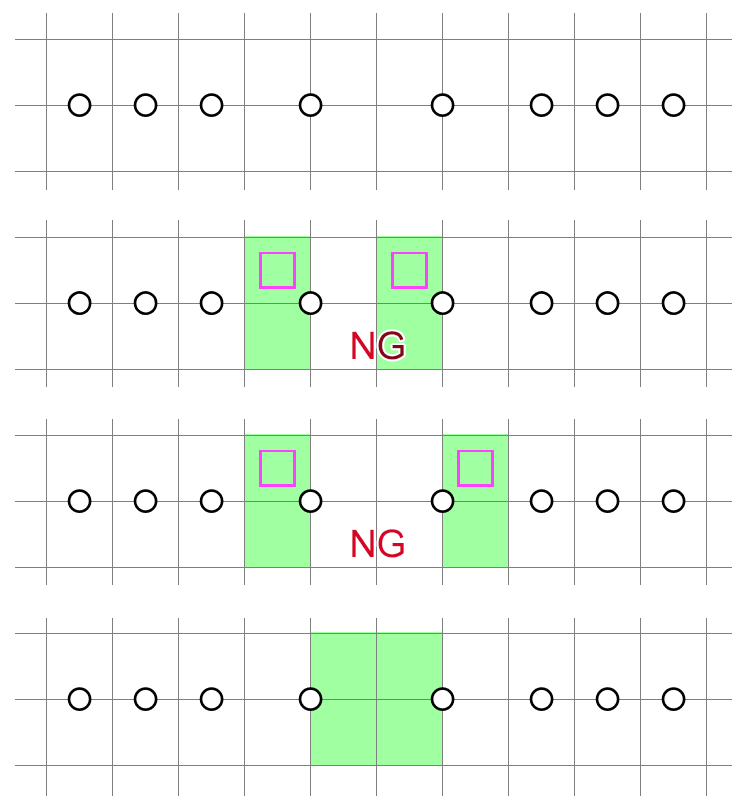
The argument for the next example follows roughly the same pattern. Two-layer lookahead leads to violation forms that we now know are impossible to shade without trying. Then apply the reasoning symmetrically.

Footnote 1: The 1-3-1 violation form had probably been used on Puzzle Square JP, but not formalized, before I gave it the name. The other two violation forms were discovered by me.

Footnote 2: There has got to be something metaphysical about how in a pencil puzzle literally called "No Three," there are three (known) violation forms that all contain 3 in 2x3's, right...? I can't put my finger on it.

Miscellaneous

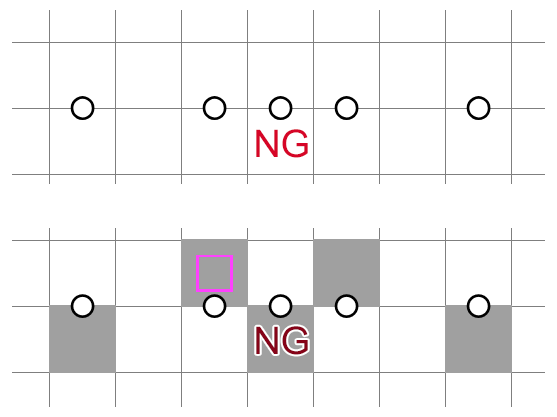
Some uncommon deductions in two rows. First, here is a structure akin to anti-mirroring (NT2/3), but it's skewed to one side:

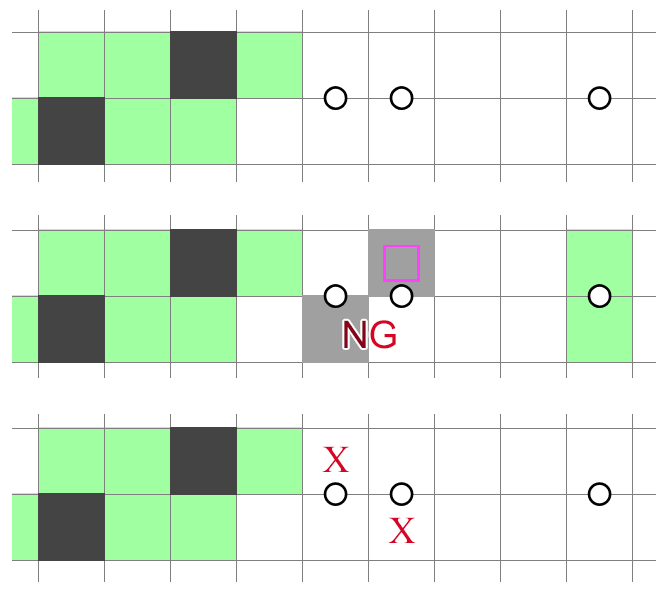
It's somewhat more expensive than anti-mirroring due to the specific shading pattern on the left.

The same idea can be compressed into NT1/2, but now it's very costly:

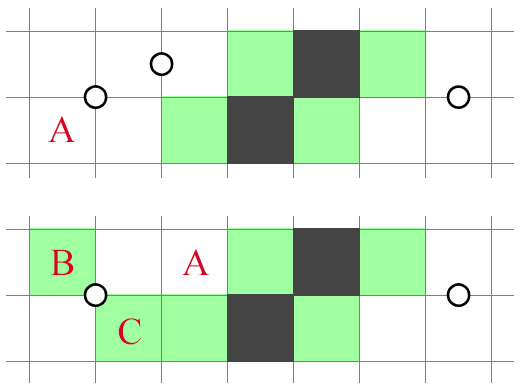
There's little you can do with the information that $A$ must be unshaded, not to mention that $B$ and $C$ need to be unshaded through external influences.

If you research NT1/2 and similar NT deductions in two rows, there's a whole class of other deductions, most of which are expensive and long. I will give just one example:

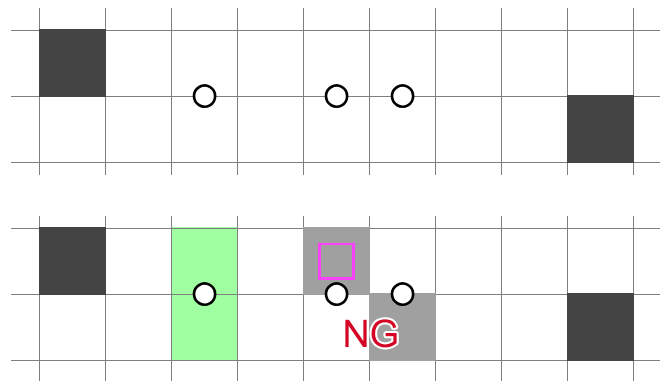
Three-Line Deductions and Above?

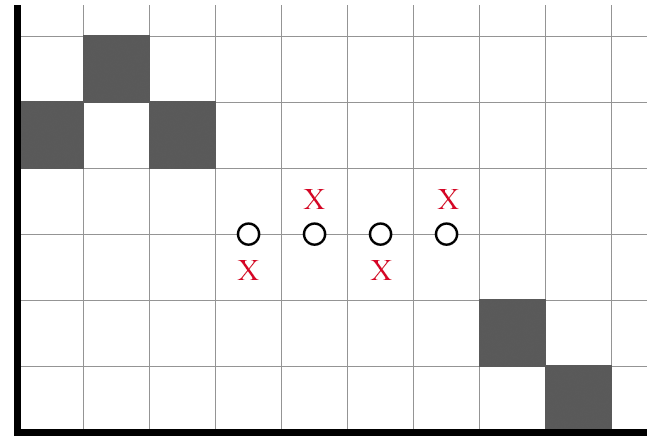
It is unclear to me whether any NT deductions involving three lines deserve attention. I have rarely encountered such deductions, particularly not cheap ones, so this is another possible direction for research. Here is the best example I could come up with:

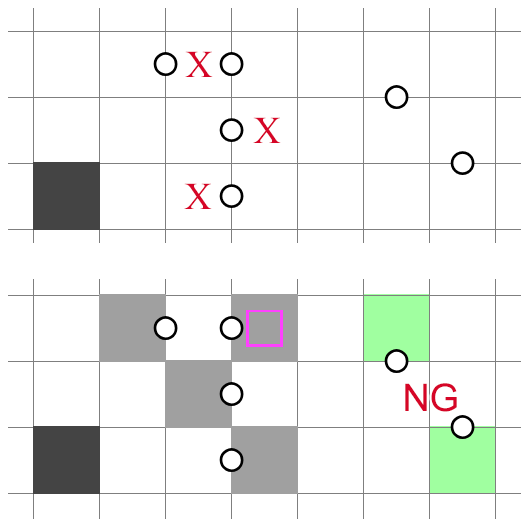
It is a three-line deduction in the sense that any two rows alone are not sufficient to determine the shading.

Penalty Theory

The penalty theory in Heyawake is about fitting as many shaded cells as possible into a given area (Here and here are good resources on the subject). As a Dynasty genre, No Three certainly incorporates this theory. Whereas in Heyawake you can simply make a big room and assign a large number, in No Three you have to pre-divide the room for the solver. This leads to complications, for you have to avoid subdividing the room into cramped structures that can be determined locally -- bypassing penalty and defeating the purpose altogether. The end result often involves patterns of alternating intersection clues and edge clues in some shape or form, like so:

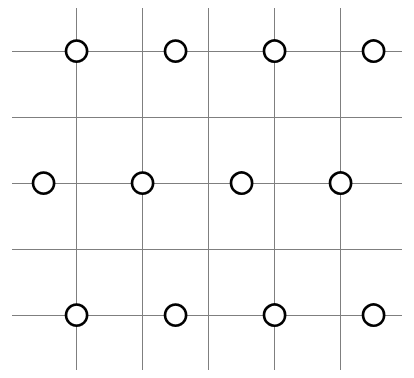
This actually makes intuitive sense. The key idea of penalty theory is that one shaded cell "breaks" three "cycles," and the initial number of cycles in an $r \times c$ grid is $(r-1)(c-1)$. Thus, the ratio between the maximum number of shaded cells in a grid and the total number of cells (as the grid size grows) is approximately $1/3$ -- in other words, you can shade about one out of every three cells in a Dynasty puzzle at best. This value is reflected in the pattern in the figure above as the two types of rooms have the average density of around $1/3$.

Of course, No Three has an additional NT rule that limits the ultimate density of shaded cells, which makes the topic too convoluted to reason about. Therefore, I will end here with a brief comment about the edge penalties on small boards. Obviously, an edge of odd length (5 cells or more) cannot be fully utilized, so there is a minimum penalty of 1 per odd-length edge. But an even-length edge of 10 cells or more cannot be fully utilized either, leading to at least 1 penalty per edge.

Double Coverage

Having discussed connectivity and NT at length, it might seem like there's nothing else fundamentally different that the genre has to offer. However, in the unassuming rule of "A circle overlaps exactly one shaded cell" lies a new kind of deduction present in few other genres. In No Three, a region can be "clued" more than once by intersection clues and edge clues; which is unlike, say, Heyawake, where each room can only be given a single number. The following trivial example illustrates what I mean:

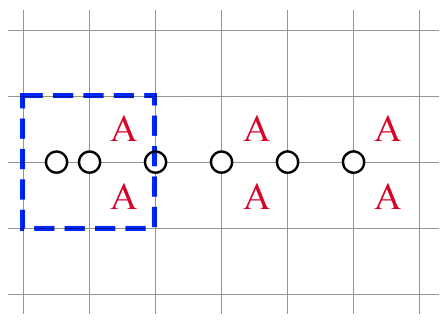
In the figure, the blue region is clued twice: once by the intersection clue, and again by the edge clue. By comparing these clues, we can conclude that there must be no shaded cells in the right half of the region. This pattern can be extended indefinitely towards the right by a series of intersection clues, forming unshaded stripes.

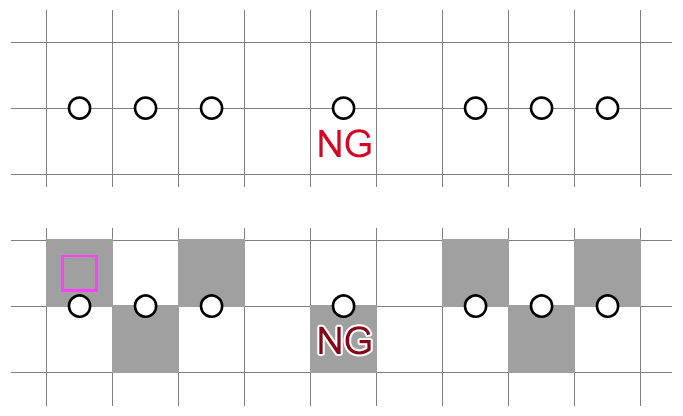
Needless to say, if that were it, we wouldn't need to talk about the deduction, let alone give it a name. The real significance of regions that are clued multiple times is that they can extend to larger, less obvious structures. The following is an invalid 4x4 construction I (arbitrarily) call "The Eye":

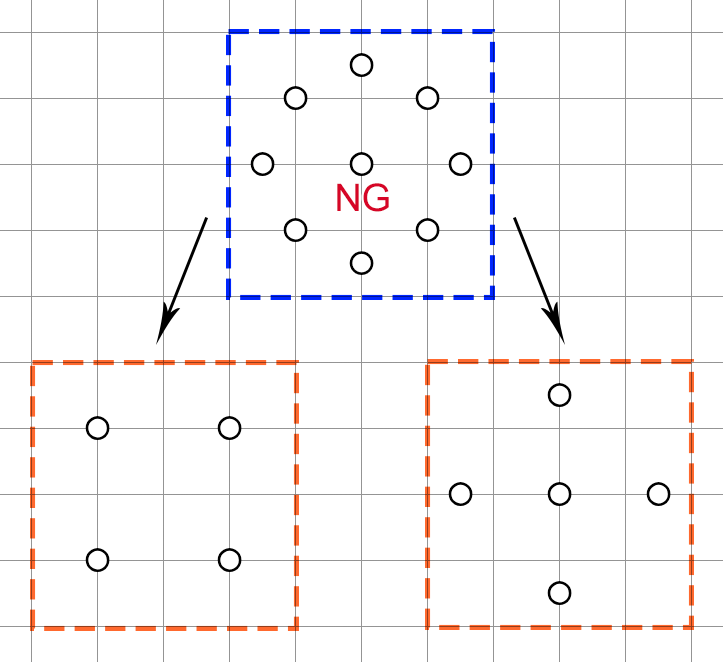
If you try to make sense of the structure in terms of the deductions we have previously discussed, you're out of luck. In fact, it doesn't use NT whatsoever. A lookahead will confirm that this structure is indeed impossible to shade; but the better view is to decompose it into two sets of clues that cover the same region, as shown in the figure. The left orange box tells us that there are 4 shaded cells in the entire region, while the right orange box tells us that there are at least 5. The numbers clearly do not match.

To implement this structure in an actual puzzle, we can remove any circle. For instance, the central circle:

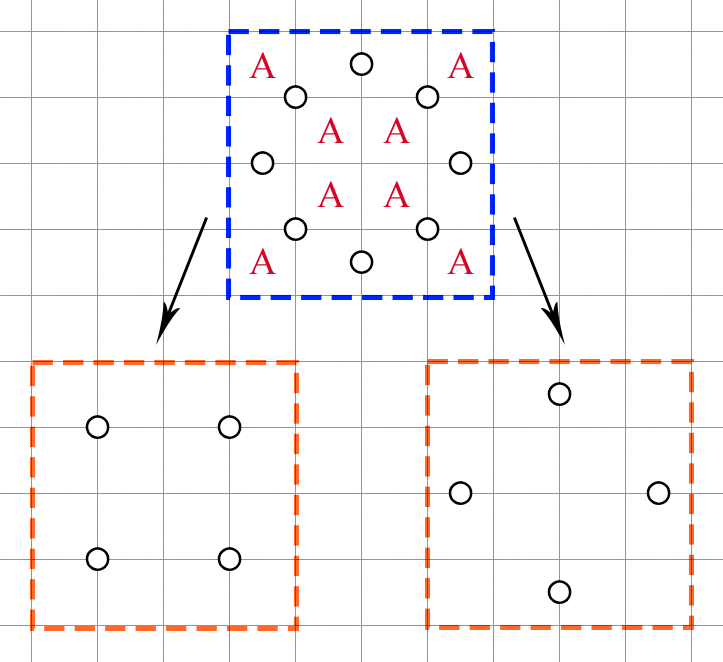
Now the decomposition gives us something that matches. We can conclude that 8 cells within the region, including 4 in the middle, must be unshaded. The remaining undecided cells constitute a binary structure. Unfortunately, if we're the setter, the 4 middle cells won't help us much. The corner cells can be used, though.

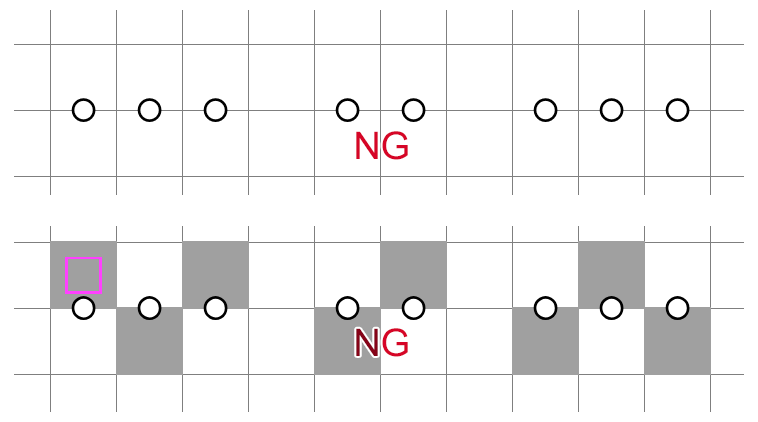
Another instance is if we remove the bottom circle instead:

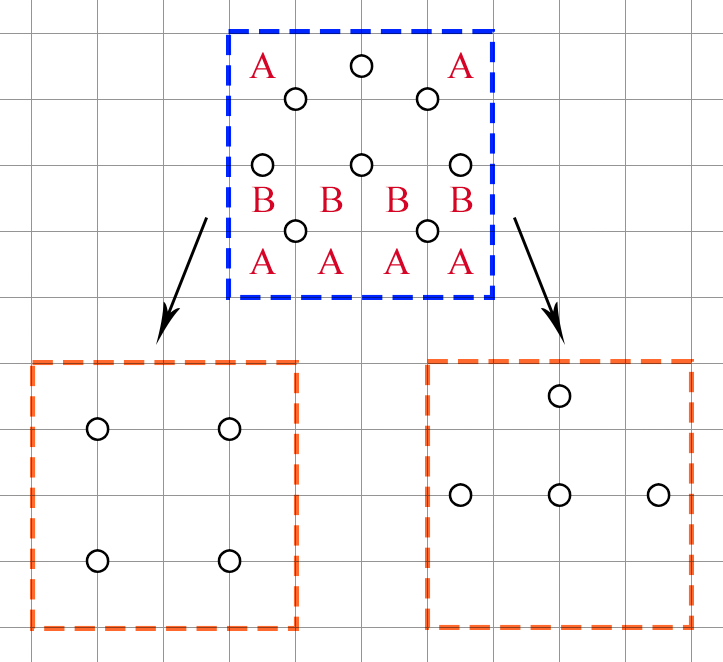
The decomposition lets us to compare the two coverings and unshade 6 cells this time. Additionally, since there are 2 shaded cells in the region marked as $B$, we essentially have a 2 in 1x4 room to combine with any other deduction we want. That said, it's worth noting that we don't really need the bottom row in this case. We can shrink the region to 3x4 and still retain the $B$ deduction.

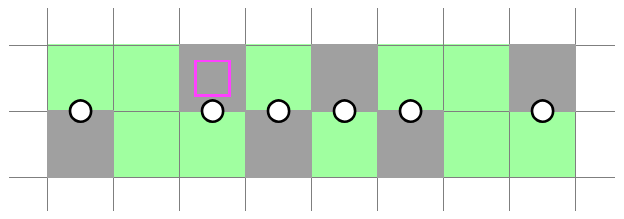
What if, instead, we have the bottom right clue removed in The Eye?

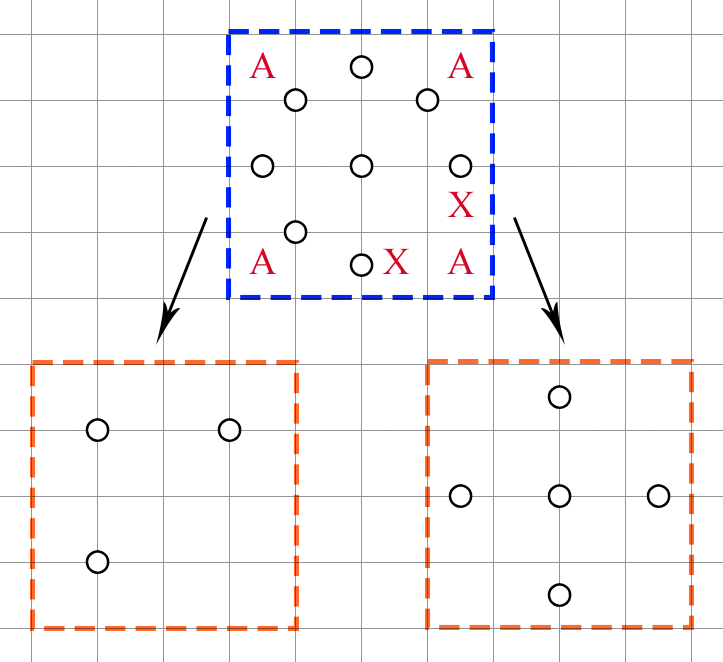
The decomposition reveals that there are at most 5 shaded cells in the left orange box, but at least 5 in the right orange box. Therefore, we know that there must be exactly 5 shaded cells in the region, with the corner cells being unshaded and the lower right 2x2 bearing 2 shaded cells. This enables us to shade 2 cells as indicated in the figure, leaving the rest of the structure undecided.

You should be able to the key idea behind double coverage at this point. We take two disjoint sets of clues to cover the same region, one giving the upper (or exact) bound, and one giving the lower (or exact) bound. In principle, the set giving the upper bound should be as sparse as possible, consisting primarily of intersection clues. On the other hand, the set giving the lower bound should be rather dense, comprising many edge clues.

A common issue with double coverage is that the clues overlap in such a way that bypasses the whole deduction. Thus, designing the pattern of clues is a delicate task. As a rule of thumb, you should not place an edge clue right next to an intersection clue (which unshades 2 cells), and edge clues should be spaced appropriately lest the solver leverage the N in 2xN. You may find that there aren't that many possibilities for double coverage after all. For truly unique patterns, you may need an area as large as 4x6 or more.

Footnote: The easliest known use of double coverage on Puzzle Square JP was by ねーじゅ in a 10x10 region. I discovered that it could be applied to much smaller regions.

Band Theory

Finally, let's examine a highly specific layout where there are nothing but intersection clues over a large area:

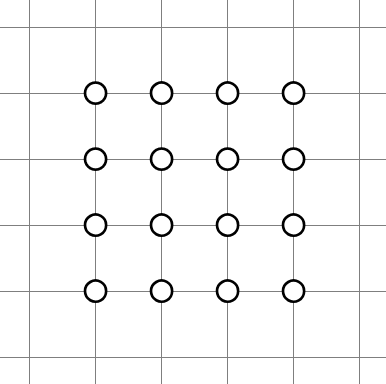
A quick investigation shows that all of our previous analysis methods fail. If we resort to lookahead, we'd need several layers of it, which is suboptimal. It's clear that a new theory is needed to better handle and understand this class of constructions. Band Theory provides an answer.

Band Theory deals with a rectangular matrix of $M \times N$ intersection clues, covering an area of $M+1$ rows and $N+1$ columns. For example, depicted in the figure above is such a matrix with $M = N = 4$.

In practice, the layout may not be rectangular, or there may be holes dug in the matrix. This tends to complicate the problem, so it is recommended to look for the largest matrix within the layout and apply Band Theory in that region, optionally with additional lookaheads. For simplicity, we will assume that we have a perfect $M \times N$ matrix.

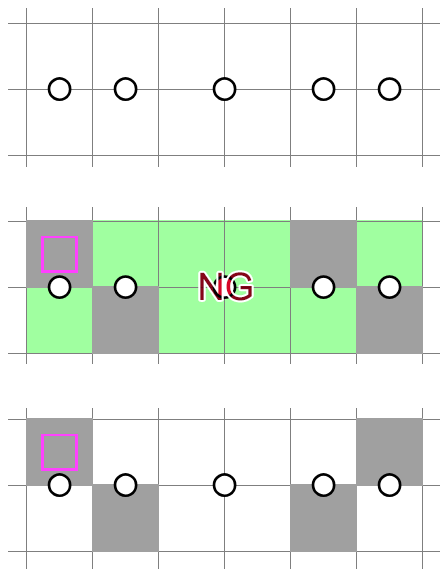
Claim: The final shading pattern will consist of either horizontal or vertical bands of shaded cells, separated by 1 cell.

Proof: To further simplify the problem, let's IGNORE the NT rule for a moment (it will be considered later). Also, to illustrate the point clearly, I will draw a large matrix, but the reasoning applies to any $M$ and $N$, even if they are small. We will consider how to shade the first two rows.

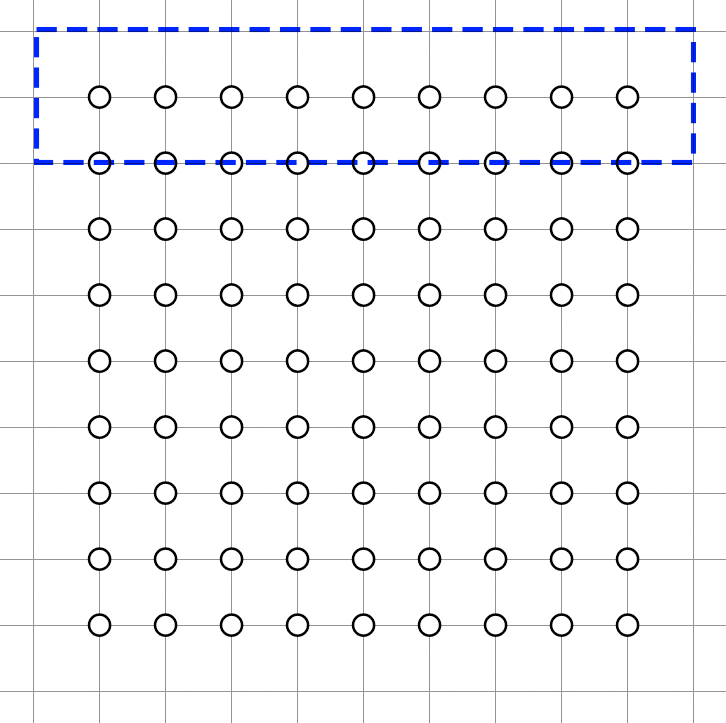
For starters, notice that in the first two rows, the columns will alternate between shaded and unshaded. This is because if we shade a cell in any column, the unshaded stripes will propagate towards the left and right. As a result, a shaded cell will take up every other column.

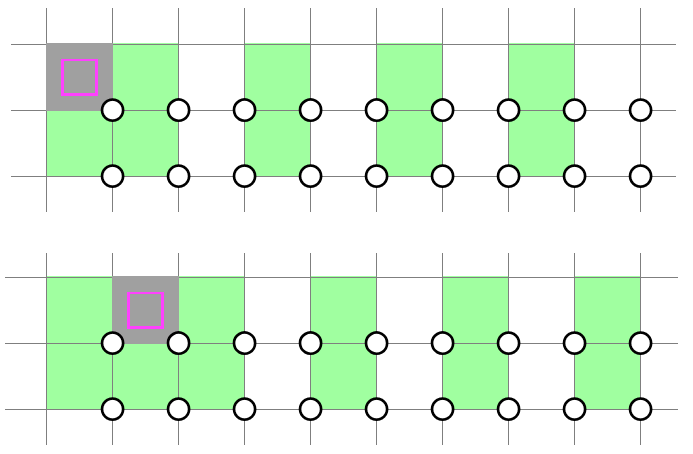
Based on this observation, we can divide the shading of the first two rows into 2 cases.

• Case 1: All shaded cells in the first two rows are in the same row.

  In this case, the row immediately below the shaded row must be completely unshaded. Next, due to the downward propagation of unshaded stripes, we are forced to alternate between shaded rows and unshaded rows, like so:

  

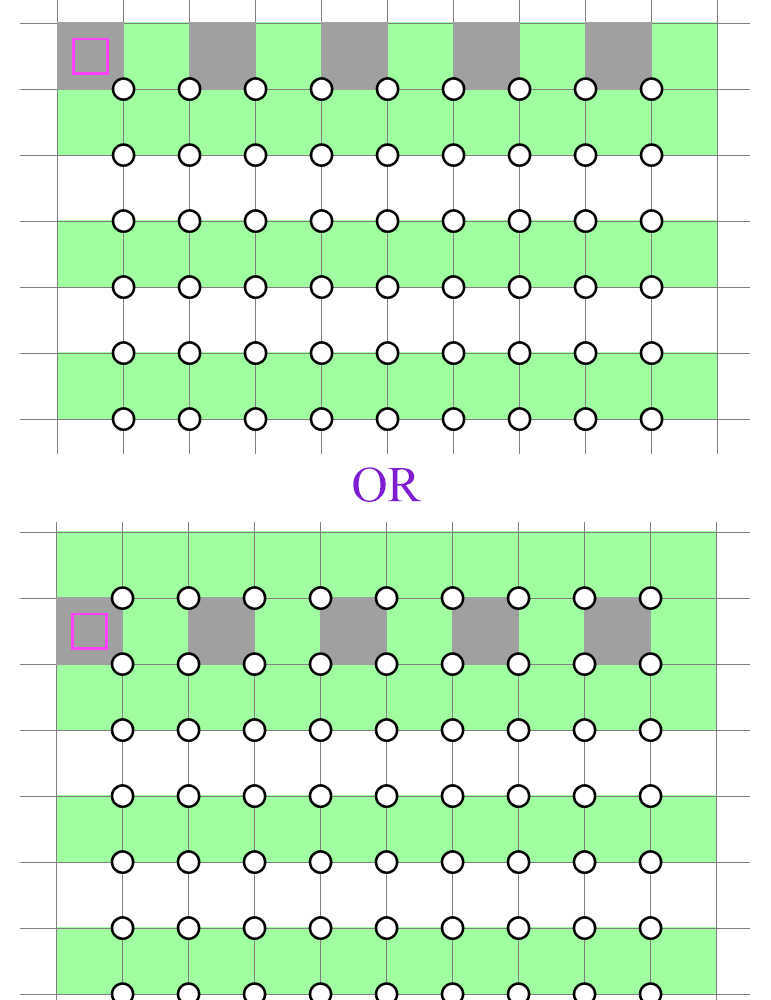
  You should now see why it's called the Band Theory: horizontal bands of shaded cells are formed in every other row. As the bands are all independent of each other, we are free to shift each band horizontally by 1 cell or not, yielding two possibilities per row. The figure below depicts a valid shading pattern (disregarding the NT rule):

  

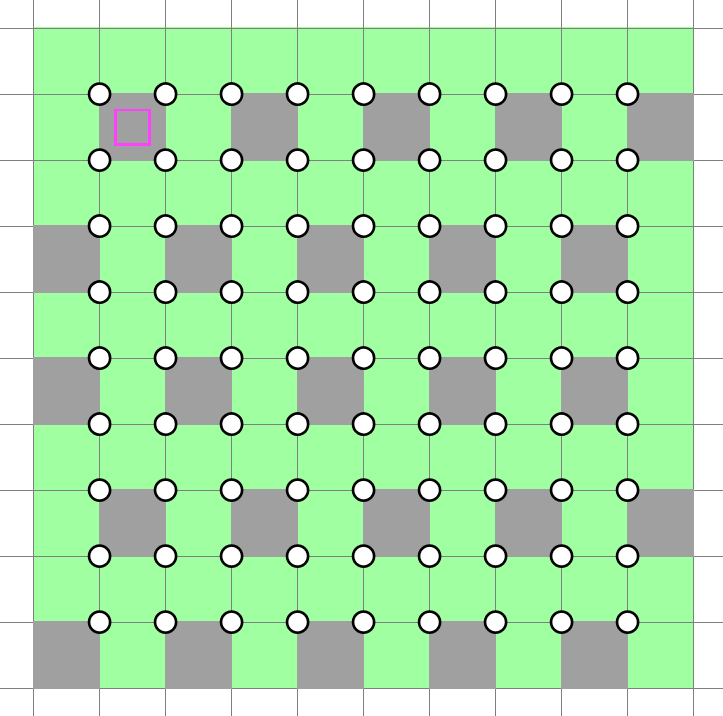
  We can also figure out mathematically the number of possible shading patterns in the case of horizontal bands. Assuming $M+1$ is even, there are $2 \times 2^{(M+1)/2}$ different patterns (only a small modification is required for when $M+1$ is odd). Not that we need this result puzzle-wise.

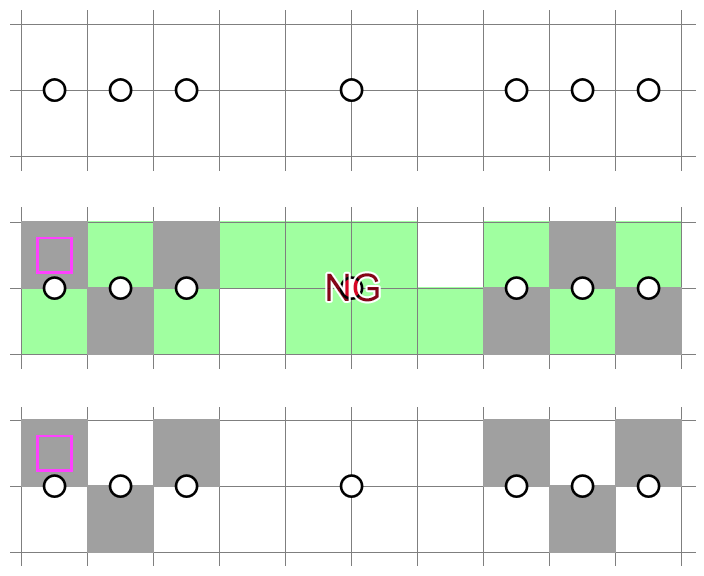
• Case 2: Not all shaded cells in the first two rows are in the same row.

  In this case, since some cells reside in row 1 and others in row 2, there must be a point at which we switch from row 1 to row 2, or vice versa. Here is one such possibility:

  

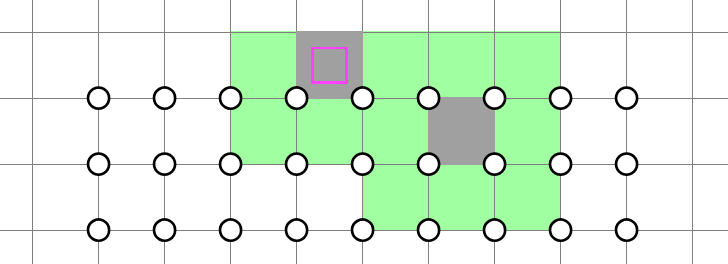
  We notice that the row 3 cell in the same column as the row 1 cell is decided, so we shade it:

  

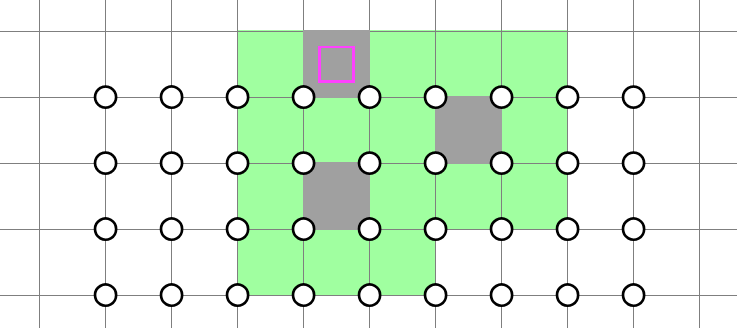
  Then, the row 4 cell is decided, and so on and so forth. This process continues indefinitely until we reach the bottom:

  

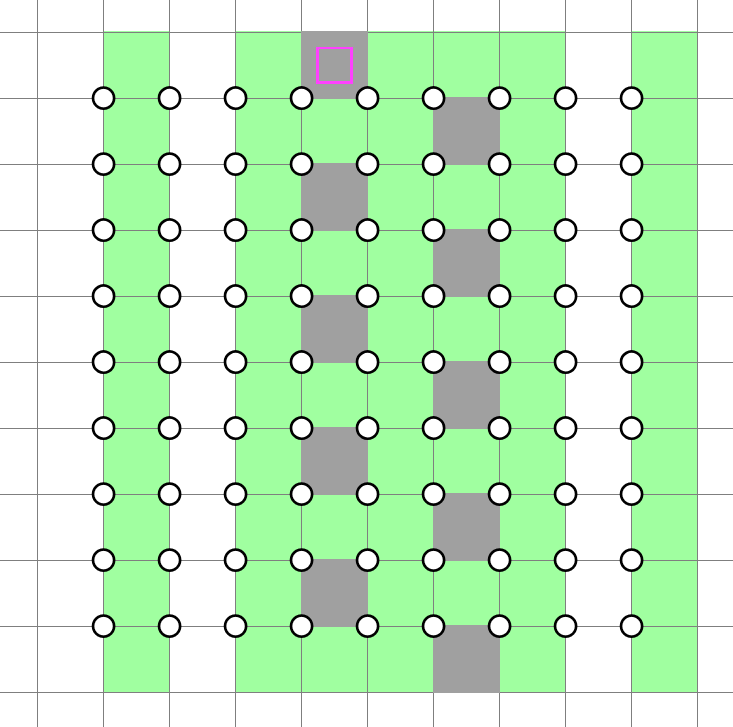
  At this point, due to the propagation of unshaded stripes to the left and right, we are forced to alternate between shaded columns and unshaded columns. Independent vertical bands of shaded cells are formed in every other column.

This concludes the proof. All in all, we have somewhere around $2^{(M+3)/2} + 2^{(N+3)/2}$ different shading patterns (varying depending on the parity of $M$ and $N$), which may shed some light on why we don't consider the scenario where there are holes in the clue matrix. Because if you remove even a single clue, the number of valid patterns would skyrocket, which can easily become unmanageable.

It's time to bring back the NT rule and consider how the theory applies in the actual No Three setting.

First and foremost, if we choose to have horizontal bands (the following argument applies symmetrically to vertical bands), then $N$ must be at most 4. If $N$ were, say, 5, then any potential horizontal band would cause an NT violation:

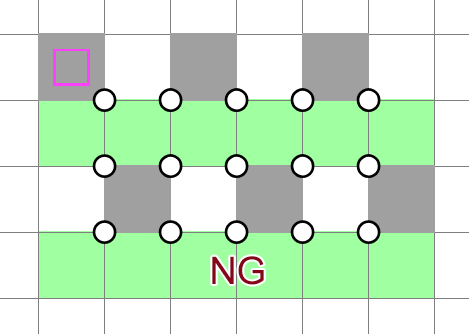
In other words, if a rectangular matrix of $M \times N$ intersection clues has a solution, then either $M \leq 4$ or $N \leq 4$ (or both), since we must have either horizontal or vertical bands.

Secondly, if we pick horizontal bands and $N = 4$ (it applies symmetrically to vertical bands), then each band must consist of two shaded cells in the middle:

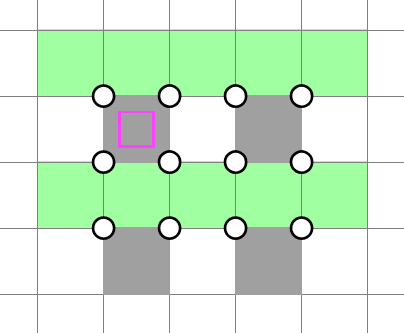
Using these results, we can solve the construction at the beginning of the section, where $M = N = 4$. The first step is to decide whether we want horizontal of vertical bands. What happens if we pick horizontal?

The bands can go along either odd or even rows. If they take the odd rows, then this is an NT violation:

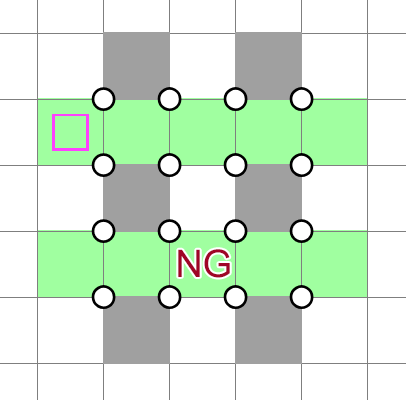
Therefore, the bands must take the even rows, which gives us a solution:

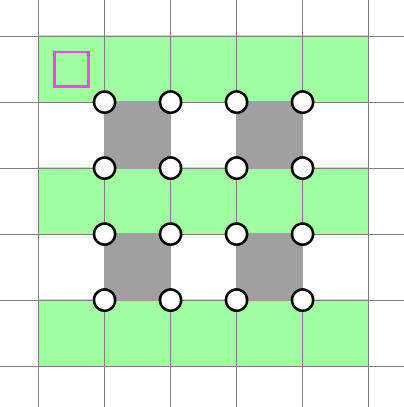
If we picked vertical bands instead, we would arrive at the same solution. This means that $M = N = 4$ has a unique solution. Furthermore, we can prove that $\{M, N\} = \{4, 5\}$ does not have a solution.

Footnote: Band Theory was first used on Puzzle Square JP by 𝕘𝕟𝕦𝕝𝕝; I formalized and proved it.

Summary

Since its humble beginnings on Puzzle Square JP in August 2023 to its appearance in the 2023 Advent Calendar, No Three has seen significant development and a surge in popularity in less than half a year. I have been fortunate enough to witness nearly the entire journey, and I feel grateful to be able to share what I have learned with the world. At this point in time, No Three is still a relatively obscure pencil puzzle compared to many others; however, I do hope that more people will stumble upon it and give it a try in the years to come. And who knows, maybe there will be more discoveries about the genre we are not yet aware of.

I sincerely appreciate you taking the the time to read such a long post. If you have any comments or suggestions, please reach out to me on Twitter @GreaterOrEqual0. In the meantime, please enjoy No Three!